Lens Selection to Optimize Camera Resolution

Sam Liebo - Lead Applications Engineer

April 2018

When choosing a lens, you need to look at two things:

1. Lens resolutions relative to pixel size on the camera

2. Max image format on the lens relative to that of the camera

For resolution it doesn't matter how many megapixels a camera lens has. All that matters is the physical size of the pixels on the camera, or more exactly, the pitch between the pixels. Every camera manufacturer will publish this information. In order to see anything, you actually need two pixels because you need to see a transition or contrast. This is know in the industry as the resolution limit or Nyquist frequency, which is the minimum distance between two lines where each can still be distinguished, commonly measured in line pairs per millimeter (1p/mm).

To calculate the minimum 1p/mm require of a lens to give you full camera resolution, use the formula:

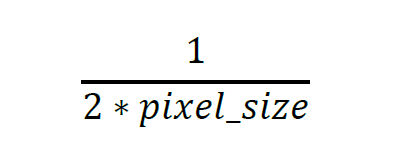
Take for example the standard 5MP 2/3" imager that has pixels 3.45 um in size. This is the sensor in the Cognex IS5705, Imaging Source DMK 33GX264e, and Basler acA2440-3um (the 5MP cameras I'd recommend). In this case, the Nyquist frequency would be:

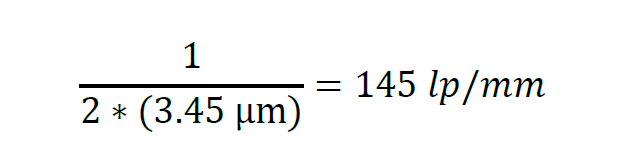
So, you'd need a lens that offers 145 1p/mm resolution or more. Its worth noting that when presented the resolution in mm or um, to calculate the 1p/mm of a lens you need to include the variable for magnification: 1/(resolution*mag).

There are two ways to determine the 1p/mm from on a lens. Either it will be published in the spec like http://moritex.com/model/1-1-2-4-4-05.html or you'll need to ask for the MTF chart. Reading an MTF chart is getting pretty deep and at that point I recommend you contact Automation, Inc. and save yourself some effort.

For reference, here is an example of MTF chart...

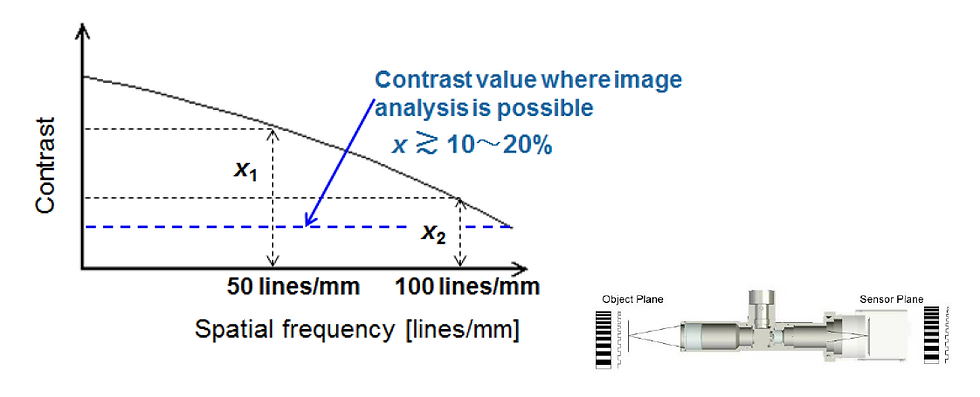
The Y axis is MTF which is the % contrast and the X axis is the frequency function given in 1p/mm. Consider this in terms of a resolution line chart (see right), where the higher frequency or "closer" spaced lines require higher resolution.

The top black line is the Diffraction Limit which is the theoretical limit of the lens performance. The different color curves represent the performance at different positions in the field of view. The better a lens is the closer these curves, in general, will be to the diffraction limit, and the tighter the curves are together the better the resolution is over the entire field of view.

This isn't an exact science (vision never is) with the constant evolution of software and may depend on application, but the rule of thumb to follow the curve to the position where the 1p/mm is at 0.15 MTF, or 15% contrast, which should be the min contrast required for measurement. So, for the MTF chart above it looks like we are a little below 1501p/mm which means we are covered for the 5MP example.

---

Sizing for image format is much simpler. The image format on the lens has to be equal to or greater than the image format on the camera. Image format is sometimes (incorrectly) called sensor size. It's the 1/3", 2/3", etc. number that you see. This is not the actual sensor size. It's a bucket that similar sized sensors fit into as a category that is confusingly named with dimension in inches.

There is historical significance to the naming (spawning from the standard size vacuum tubes...aka pre-semiconductor science). Basically, if you use a 1/2" lens (like http://moritex.com/model/1-1-2-4-3-01.html) on a 2/3" sensor (like the 5MP above) you will get darkening of the corners of your image as the lens is not large enough to cover the full sensor. This is known as vignetting.

The biggest mistake I see with lens selection is people just look at the image format and assume that if a lens says 2/3" then it can handle a 5MP 2/3" camera. That is not taking the size of the pixels into account at all and may leave you with a less than ideal image. It's not worth saving $100-$200 on a lens if you already spent the money on a high-resolution camera. If you don't need high resolution, then go with a low-resolution camera (or you pay for empty performance).